Carambolas.

El billar francés, o el juego de las carambolas, que
probablemente proviene del siglo XVIII, se juega
en una mesa sin orificios. Lo entretenido del juego
es el cálculo preciso de las trayectorias al golpear
las bandas de la mesa antes de alcanzar las bolas.

Se dice que algo sucede "de carambola” cuando, contra todo pronóstico, se produce la confluencia de varias circunstancias inesperadas. Varios efectos coinciden y parece deberse sólo al azar. 

Diagrama interior del libro de Coriolis.

La carambola es también el juego del billar francés, que consiste mayormente en alcanzar un par de bolas de colores con otra blanca. Si bien, esa bola blanca previamente debe rebotar en varias bandas de una mesa que carece de huecos. Pero en el billar, aunque también hablemos de carambolas, casi nada es azar. La carambola sólo sucede después de un profundo análisis geométrico y una ejecución precisa para predecir su comportamiento tras el golpeo.  El billar incita nuestro deseo ancestral de dominio sobre lo contingente. Sobre la mesa de billar pensamos igual que lo hacemos en otros ámbitos de la vida, cuando intentamos predecir la inconmensurable concatenación de procesos de causa y efecto. Aunque a menudo ese análisis nos supere.

Y sin embargo, a quien sabe poco del asunto puede que le asombre la cantidad de predicciones que sobre una mesa de billar se pueden hacer, por supuesto, echando mano de la geometría y la física. Ya en 1835, el maestro de la politécnica, Gaspar Gustave de Coriolis, escribió la obra titulada “Teoría matemática del juego de billar”. Y en ella se estudiaba algo tan minucioso como las trayectorias parabólicas de las bolas. 

Si bien, nosotros nos ocuparemos de aspectos más simples, y en verdad, sólo aquellos relacionados con la SIMETRÍA y los ángulos de reflexión. Vamos a ver que las bolas, en sus trayectorias más comunes, sugieren de nuevo el problema de Herón de Alejandría, que vimos en la clase pasada.


El problema de la mesa de billar. Problema 1. 

Nuestro primer problema consiste en golpear a una de las dos bolas que se encuentran en la mesa (la A por ejemplo) , de forma que ésta impacte con la otra (la bola B) dando previamente en una de las bandas (bordes) de la mesa.

En el siguiente grafo se detalla el problema, que puede enunciarse de la siguiente manera:

Determinar la dirección “d” con la que debemos golpear en el centro de la bola “A” para que, tras impactar en la banda de la mesa en un punto “P” a determinar, rebote e impacte con la bola “B” situada en otro punto de la mesa.

La posible trayectoria (APB) ha sido representada con líneas discontinuas.

Recordaremos que en un rebote, el ángulo de incidencia, alfa, respecto a la superficie es igual al ángulo con el que sale despedida la bola. En verdad, estamos ante un problema de simetría. Veamos si somos capaces de resolverlo.





El problema de la mesa de billar. Explicación y solución del problema. 

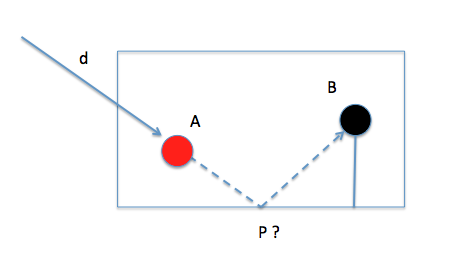
Al plantear el problema de la mesa de billar, que consiste en golpear a una de las dos bolas que se encuentran en la mesa (la A por ejemplo) de forma que ésta impacte con la otra (la B) dando previamente en una de las bandas (bordes de la mesa), dejábamos el problema cerrado a un caso de simple rebote, es decir, en una única banda.

Podemos generalizar el problema considerando que se pueden dar, antes de impactar con la segunda bola, un número determinado de impactos con las bandas (bordes laterales) de la mesa, pero para simplificar el análisis lo resolveremos primero en el caso más sencillo: una sola banda.

Supondremos además una posición genérica de las bolas sobre la mesa de juego, de forma que no tengamos situaciones particulares que puedan conducir a soluciones singulares. En la siguiente figura se esquematiza un posible caso de estudio.

El objetivo o solución del problema es determinar un cierto punto “P” sobre la banda, donde debe rebotar la bola “A” antes de impactar con la bola “B”. La dirección “d” por tanto con la que lanzaremos la bola A quedará determinada por la recta AP.

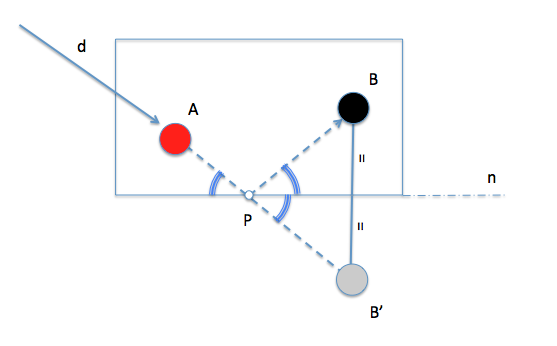
Para resolver el problema obtendremos el simétrico del punto “B” respecto de la banda “n” en la que se encuentra el punto “P” buscado. Este punto simétrico al que llamaremos ” B’ ” nos permitirá obtener la dirección d ya que el ángulo en P que forman las rectas “n” y PB’ es el mismo que el que forman “n” y “PB” por ser el triángulo PBB’ isosceles y la recta “n” coincidir con su altura sobre el lado BB’.

Por otra parte sabemos que los ángulos que forman dos rectas AP y “n”, por ejemplo, en el punto “P” a un lado y otro son iguales al ser opuestos por el vértice.

En la figura se han marcado estos ángulos (iguales) por lo que el rebote cumpliría con las reglas de la reflexión tal y como se proponia en el enunciado del problema.

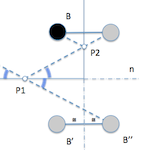
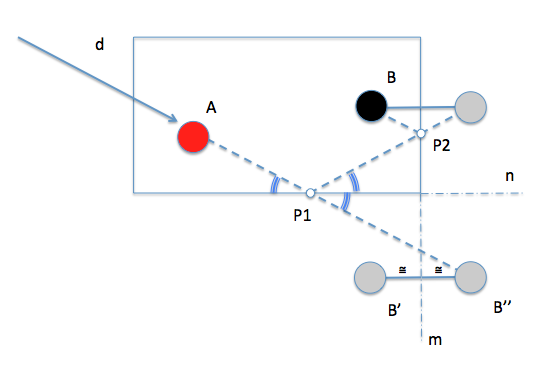
Para generalizar el problema a varias bandas introduciremos una nueva condición de rebote sobre otra banda, la “m” por ejemplo. La solución nos llevará de nuevo a plantear simetrías para conservar los ángulos en el rebote de las bandas. En este caso deberemos realizar la simetría del caso anterior y a ésta añadirle una nueva respecto de la banda “m”. El nuevo punto ” B” ” nos permitirá determinar la trayectoria inicial y obtener el punto de impacto en la primera banda (P1), desde el que resolveremos el nuevo punto (P2) por reducción del problema al modelo anterior.

Ahora se trataría de plantear problemas distintos a dos bandas. Y llegado el caso, resolver los problemas a tres bandas. A mi se me ocurren varios, pero los plantearé ya sobre la pizarra, en el aula, que se me hace tarde por hoy. 

Buenas noches, corianitos. 

Soluciones de trayectorias a 1, 2 y 3 bandas. 

e

Por último, traigo un problema de billar más complejo, en este caso realizado sobre una mesa circular. Está resuelto con homotecia y potencias.